欧拉路径

总结下欧拉路径相关的算法。

欧拉图判定

无向图

一个无向图是欧拉图当且仅当该图是连通的（注意，不考虑图中度为0的点，因为它们的存在对于图中是否存在欧拉环、欧拉路径没有影响）且所有点的度数都是偶数；一个无向图是半欧拉图当且仅当该图是连通的且有且只有2个点的度数是奇数（此时这两个点只能作为欧拉路径的起点和终点）。

原理：因为任意一个点，欧拉环（或欧拉路径）从它这里进去多少次就要出来多少次，故(进去的次数+出来的次数)为偶数，又因为(进去的次数+出来的次数)=该点的度数（根据定义），所以该点的度数为偶数。

有向图

一个有向图是欧拉图当且仅当该图的基图（将所有有向边变为无向边后形成的无向图，这里同样不考虑度数为0的点）是连通的且所有点的入度等于出度；一个有向图是半欧拉图当且仅当该图的基图是连通的且有且只有一个点的入度比出度少1（作为欧拉路径的起点），有且只有一个点的入度比出度多1（作为终点），其余点的入度等于出度。

欧拉路径判定

无向图

一个无向图存在欧拉路径，当且仅当该图所有顶点的度数为偶数或者除了两个度数为奇数（这两个点是欧拉路的起点和终点）外其余的全是偶数。

有向图

一个有向图存在欧拉路径，当且仅当该图所有顶点的度数为零或者一个顶点的度数为 $1$，另一个度数为 $-1$，其他顶点的度数为 $0$。

欧拉路径求法

根据上面叙述的欧拉路径的判定条件，不难想到，对图做一次DFS遍历便可以得到欧拉路径，复杂度为 $O(2M)$。具体做法如下：

对于无向图，如果度数为奇数的顶点恰好有两个，那么从这两个点中的任何一个点开始DFS，最终一定会到达另一个度数为奇数的顶点。如果度数为奇数的顶点个数为0，那么从图中的任何一个点出发，都能找到欧拉路径。

对于有向图，做法无向图中的算法类似。需要注意的是，如果图中有一个顶点度数为1，另一个顶点度数为-1，那么需要从那个度数为1的顶点开始DFS遍历。

举例

下面举出两个需要求解欧拉路径的题目。

SGU 101

题解：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <list>
using namespace std;

struct Edge {
    int x, y;
};
const int maxn = 105;
Edge edge[maxn], path[maxn];
int mat[10][10];
int n, x, y, start = 0, flag = 0, degree[10], p = 0;

void dfs(int s) {
    for(int i = 0; i <= 6; ++i) {
        if(mat[s][i]) {
            mat[s][i]--; mat[i][s]--;
            dfs(i);
            p++; path[p].x = s; path[p].y = i;
        }
    }
}

inline void output() {
    for(int i = p; i >= 1; --i) {
        for(int j = 1; j <= n; ++j) {
            if(edge[j].x == path[i].x && edge[j].y == path[i].y) {
                edge[j].x = -1; printf("%d +\n", j); break;
            }
            else if(edge[j].x == path[i].y && edge[j].y == path[i].x) {
                edge[j].x = -1; printf("%d -\n", j); break;
            }
        }
    }
}

int main(int argc, char** args) {
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i) {
        scanf("%d %d", &x, &y);
        edge[i].x = x, edge[i].y = y;
        degree[x]++; degree[y]++;
        mat[x][y]++; mat[y][x]++;
    }
    for(int i = 0; i <= 6; ++i) {
        if(degree[i]) {
            start = i; break;
        }
    }
    for(int i = 0; i <= 6; ++i) {
        if(degree[i] % 2 == 1) {
            flag++; start = i;
        }
    }
    if(flag!=0 && flag!=2) {
        printf("No solution"); return 0;
    }
    dfs(start);
    if(p < n) {
        printf("No solution"); return 0;
    }
    output();
    return 0;
}

这题有两个地方需要特别注意：

(1). 完成DFS之后，还需要进一步判断图是否连通，即DFS过程是否经过了所有的边，这一点可以通过比较边数与DFS经过的边数来实现。

(2). 注意欧拉路径不是欧拉环！忽略这一点在DFS是会出错，例如下图：假如题目中给出的边具有几下关系：

欧拉路径

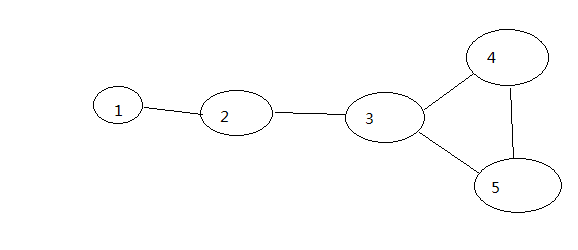
那么，从节点3开始DFS，先到节点2，再到节点1，就会陷入死循环！

这道题也可以不使用邻接矩阵记录每两个节点之间边的数目(当顶点数较多时，使用邻接矩阵来记录边的信息会占用大量的内存空间)，从边开始递归DFS，注意下压栈的顺序即可。

POJ 2337

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

struct Edge {
    char str[25];
    int start, end, len;
    bool used;
};

const int maxn = 1005;
Edge edge[maxn];
int T, n, path[maxn], p = 0;
int in[27] = {0}, out[27] = {0};

bool cmp(const Edge & a, const Edge & b) {
    return strcmp(a.str, b.str) <= 0 ? true : false;
}

void dfs(int s) {
    for(int i = 0; i < n; ++i) {
        if(!edge[i].used && edge[i].start == s) {
            edge[i].used = true;
            dfs(edge[i].end);
            path[p++] = i;
        }
    }
}

int main(int argc, char** args) {
    scanf("%d", &T);
    while(T--) {
        scanf("%d", &n); p = 0;
        memset(path, 0x00, sizeof(path)); memset(edge, 0x00, sizeof(edge));
        memset(in, 0x00, sizeof(in)); memset(out, 0x00, sizeof(out));
        for(int i = 0; i < n; ++i) {
            scanf("%s", edge[i].str); edge[i].len = strlen(edge[i].str);
            edge[i].start = edge[i].str[0]-'a';
            edge[i].end = edge[i].str[edge[i].len-1]-'a';
            edge[i].used = false;
        }
        sort(edge, edge+n, cmp);
        for(int i = 0; i < n; ++i) {
            out[edge[i].start]++;
            in[edge[i].end]++;
        }
        int start = edge[0].start, incnt = 0, outcnt = 0, flag = 0;
        for(int i = 0; i < 26; ++i) {
            if(in[i] == out[i]) {
                continue;
            }
            else if(in[i]-1 == out[i]) {
                incnt++;
            }
            else if(out[i]-1 == in[i]) {
                outcnt++; start = i;
            }
            else {
                flag = 1; break;
            }
        }
        if(flag == 0 && (incnt==1&&outcnt==1 || incnt==0&&outcnt==0)) {
            p = 0; dfs(start);
            if(p < n) {
                printf("***\n"); continue; // no euler path.
            }
            for(int i = p-1; i > 0; --i) {
                printf("%s.", edge[path[i]].str);
            }
            printf("%s\n", edge[path[0]].str);
        }
        else {
            printf("***\n"); continue; // no euler path.
        }
    }

    return 0;
}

这一题考察的是有向图的欧拉路径。

Fleury算法求欧拉路径

这个算法在实现时有很巧妙的方法。因为DFS本身就是一个入栈出栈的过程，所以我们直接利用DFS的性质来实现栈，其伪代码如下：

DFS(u):
    While (u存在未被删除的边e(u,v))
        删除边e(u,v)
        DFS(v)
    End
    PathSize ← PathSize + 1
    Path[ PathSize ] ← u

需要注意的是：必须在遍历完所有边后才能将该点加入到Path中。

相关的定义

欧拉图判定

无向图

有向图

欧拉路径判定

无向图

有向图

欧拉路径求法

举例

Fleury算法求欧拉路径

Comments: