Pell's Equation
Pell’s Equation值得是形如 \(x^2-Dy^2=1\) 的一类丢番图方程(Diophantine Equation),其中,$D$是一个正的非完全平方数。
迭代求解
对于方程$x^2-Dy^2=1$,对应的图像是双曲线,很容易观察到平凡解$(-1, 0)$和$(1, 0)$。以$D = 2$为例:
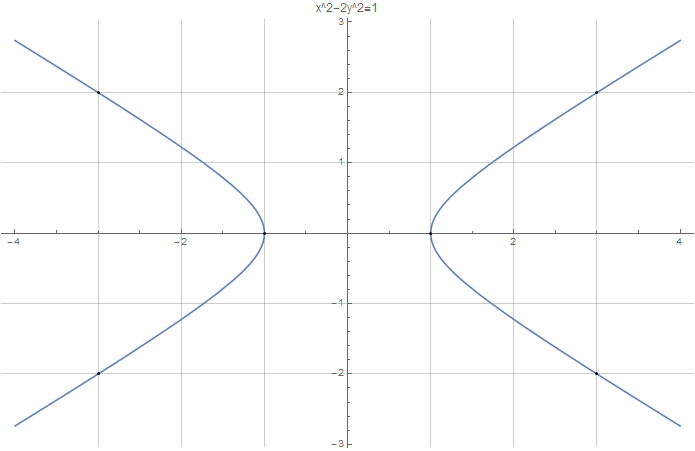
当$D$是非完全平方数时,Pell’s Equation 有无穷多组不同的整数解,方程所有的根可以通过迭代来求解。 由于方程对应的图像是双曲线,只要求解出了第一象限内的所有解,由双曲线的对称性,也就得到了所有的解。 设$(x_1, y_1)$、$(x_2, y_2)$是方程在第一象限的两个不同的根,那么,
\[(x_1^2-Dy_1^2)(x_2^2-Dy_2^2)=(x_1x_2+Dy_1y_2)^2-D(x_1y_2+x_2y_1)^2\]这意味着$(x_1x_2+Dy_1y_2, x_1y_2+x_2y_1)$也是方程的解。按照这个规律,得出推导式:
\[\begin{cases} x_{k+1} &= x_1 x_k + D y_1 y_k \\ y_{k+1} &= x_1 y_k + x_k y_1 \end{cases}\]Chakravala method
显然,如果初值取$(1, 0)$,那么只能得到$(1, 0)$这一组解。因此,需要用到Chakravala method来求解方程 最小的正整数解,作为$(x_1, y_1)$,以用来迭代求出方程所有的根。Chakravala method的做法是考虑方程
\[x^2-Dy^2=k\]设$(x_1, y_1, k_1)$、$(x_2, y_2, k_2)$都满足方程$x^2-Dy^2=k$,将这两个三元组组合起来,得到一个新的 三元组,
\[(x_1x_2+Dy_1y_2, x_1y_2+x_2y_1, k_1k_2)\]进一步求解需要用到Bhaskara’s lemma:
\[a^2-Db^2=k \implies (\frac{am+bD}{k})^2 - N(\frac{a+bm}{k})^2 = \frac{m^2-D}{k}\]而$(am+bD, a+bm, k(m^2-D))$相当于是两个三元组$(a, b, k)$和$(m, 1,m^2-D)$的组合, 因此,只要找到满足条件的$a$、$b$、$m$,按照规则
\[\begin{cases} a &\gets \frac{am+bD}{|k|} \\ b &\gets \frac{a+bm}{|k|} \\ k &\gets \frac{m^2-D}{k} \end{cases}\]迭代,当$k$的值为$1$时,也就得到了原方程的解,这个解也是原方程的最小的正整数解。
接下来需要确定$m$的初值,考虑$k$整除$m^2-D$,而$k$的初值是$1$,因此,满足条件的最小的$m$的 值为$\sqrt{D}$。在之后的每一步迭代中,需要保证$a+bm$能够被$k$整除,$m^2-D$能够被$k$整除且结果的绝对值尽量小。 要想找到符合这一条件的$m$的值,首先$a+bm$除以$k$的余数为$0$,由这一条件可以得到一系列的$m$的可取值, 然后,从中挑选一个$m^2$距离$D$最近的$M$即可。
Negative Pell Equation
Negative Pell Equation指的是方程
\[x^2-Dy^2=-1\]可以通过将这个方程变换到普通的Pell’s Equation,然后按照Pell’s Equation的方法求解,最后再得到对应的原方程的解。
\[\begin{aligned} x^2-Dy^2=-1 &\implies (x^2-Dy^2)^2 = 1 \\ &\implies (x^2+Dy^2)^2 - D(2xy)^2 = 1 \\ &\implies (2x^2+1)^2 - D(2xy)^2 = 1 \end{aligned}\]另一种思路,直接按照Chakravala method进行迭代,当$k=-1$时得到原方程的一个解。
应用实例
Project Euler的第66题和第94题都用到了Pell’s Equation。第66题要求 求解$D \le 1000$中使得方程$x^2-Dy^2=1$的解最小正整数解$(x, y)$中的$x$取到最大值的$D$。具体解题 思路,从$1$到$1000$枚举所有的$D$,求解$(x, y)$,记录最小的$x$及对应的$D$的值即可。第94题要求求解周长 不超过10亿的三角形中,边长和面积都为整数的近似等边三角形(近似等边三角形是指有两条边相等,且 第三条边与其他两条边相差不超过$1$的三角形)的周长和。最终可以等价于求解方程
\[{\frac{3a-1}{2}}^2-3h^2=1\]的所有正整数解,容易看出一个解为
\[(\frac{3a-1}{2}=2, h=1)\]只需要按照Pell’s Eqaution的规则迭代即可。