• Mar 22, 2015

    Haskell 基本输入与输出(Basic IO)

    Haskell拥有惰性求值和一切皆函数的设计，在Haskell中，函数仅仅负责根据提供的参数返回特定的结果，并且，函数的结果不受外部环境的影响，仅仅与参数有关。但IO却拥有副作用，IO环境的变化使得函数的运行状态不可预测，这对程序的流程造成了严重的潜在影响。在Haskell中，使用了一套Monadic I/O的模型来弱化和解除程序对IO操作的依赖，其基本思想是控制构造具有IO操作的程序和限制IO运算对函数的影响。

  • Mar 18, 2015

    先验和后验概率以及估计

  • Mar 2, 2015

    Logistic回归

    Logistic回归与多重线性回归类似，区别就在于它们的因变量不同。多重线性回归的因变量连续，而Logistic回归的因变量是离散的，一般为二项分布，即对应二分类问题。

    回归问题的常规步骤：

    1. 构造假设函数$h$。
    2. 构造损失函数$J$。
    3. 调整回归参数$\theta$使得损失$J$最小。

    • 2015-02

  • Feb 28, 2015

    Haskell 高阶函数

    返回函数的函数

    以求最大值的函数max'为例，

    max' :: (Ord a) => a->a -> a
max' x y
    | x >= y = x
    | x < y  = y

    调用该函数时可以这样做：

    max' 1 2

    也可以这样做：

    (max' 1) 2

    原因是这个函数的定义也可以看成是

  • Feb 26, 2015

    最大流算法

    定理

    1. 增广路定理

    对于流 $f$，若残留网络 $G_f$ 不存在增广路，则 $f$ 为流网络 $G$ 的最大流。

    1. 最大流最小割定理

    定义流网络 $G$ 的切割(cut)，为流网络的点集 $V$ 的一个划分 $[S, T]$，且源点 $source$ 在 $S$ 中，汇点 $sink$ 在 $T$ 中。从 $S$ 到 $T$ 的边称为割边。 切割的流量即从 $S$ 到 $T$ 的边的流量之和。在网络 $G$ 中 $[S, T]$ 为最小的切割，$f$ 为最大流，则有 $|S| = |f|$。

  • Feb 25, 2015

    最大公约数算法

    关于最大公约数的求解，主要有欧几里得算法和Stein算法两种方法。

    欧几里得算法

    欧几里得算法的原理为：

    若

    \[a \equiv r(mod\ b)\]

    则

    \[gcd(a,b) = gcd(b,r)\]

    算法执行过程为辗转相除法。

  • Feb 24, 2015

    树状数组

    树状数组(Binary Index Tree, BIT)，是一个查询和修改复杂度都为O(lg(n))的数据结构。

    定义

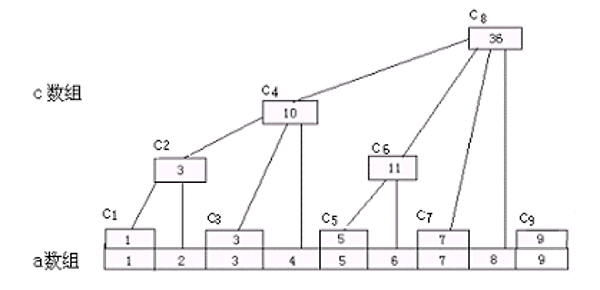
    对于序列 $a$，我们设一个数组 $C$ 定义 $C[i] = a[i – 2^k + 1] + \dots + a[i]$ ($i$ 从 $1$ 开始)，$k$ 为 $i$ 在二进制下末尾 $0$ 的个数。 $k$ 的计算可以这样:

    \[2^k = x \textit{ and } (x \textit{ xor } (x-1))\]

    树状数组的结构如下图所示：

    树状数组

  • Feb 20, 2015

    Haskell 函数

    在Haskell中，一切皆函数。

    定义一个函数

    haskell中，可以通过如下方式定义一个简单的函数：

    doubleMe x = x + x

    这样的做法其实是实现了一个绑定(binding)。更广泛的函数定义的方法：

    func1 :: Int -> String
{- function body. -}

func2 :: Int->Int -> String
{- function body. -}

func3 :: (Integral a) => a -> String

{- function body. -}

func4 :: (Integral a) => a->a -> String
{- function body. -}
  • Feb 18, 2015

    Javascript 变量作用域

    Javascript 中的变量

    Javascript 中的变量可分为全局变量和局部变量两种。

    Javascript 中使用 var 语句声明变量。例如：

    var x = 10;
var y = ["a", 20, true]

    变量相等性比较

    Javascript 中，比较两个变量是否想等是，必须注意 ==和=== 之间的区别。

    ==只比较变量的值，而 ===既比较变量的值，又比较变量的类型。如下例：

  • Feb 17, 2015

    Linux 文件解压及压缩命令

    Linux下，通常需要用tar命令进行解压和压缩操作，针对不同的压缩文件格式，tar命令的参数也不相同。

    tar 命令的常用参数含义:

    Main operation mode:

 -A, --catenate, --concatenate   append tar files to an archive
 -c, --create               create a new archive
 -d, --diff, --compare      find differences between archive and file system
     --delete               delete from the archive (not on mag tapes!)
 -r, --append               append files to the end of an archive
 -t, --list                 list the contents of an archive
     --test-label           test the archive volume label and exit
 -u, --update               only append files newer than copy in archive
 -x, --extract, --get       extract files from an archive

Subscribe via RSS

← Newer
Older →