投影与相机空间

计算机屏幕是2维的，OpenGL渲染的3D场景必须以2D形式的图像投影到屏幕上。

透视投影

透视投影能较好的使二维投影显示立体感，因为人眼观看物体符合透视原理。首先，将所有顶点从眼坐标(照相机坐标)转换到裁剪坐标系下。然后，这些裁剪坐标通过透视除法，即除以裁剪坐标中w分量，转换到归一化设备坐标系(NDC)。在透视投影中，在眼坐标下截头椎体(a truncated pyramid frustum)内的3D点被映射到NDC下一个立方体中；x坐标从[l,r]映射到[-1,1],y坐标从[b,t]映射到[-1,1]，z坐标从[n,f]映射到[-1,1]。

世界坐标和眼坐标系使用右手坐标系，而NDC使用左手坐标系。这就是说，眼坐标系下，在原点处的照相机朝着-Z轴看去，但是在NDC中它朝着+Z轴看去。如下图所示：

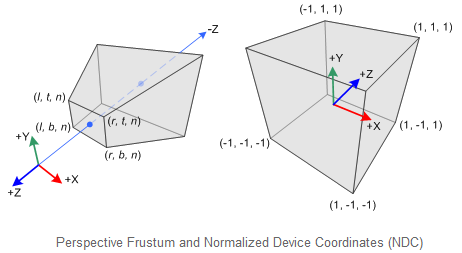
相机坐标系与设备坐标系

由几何关系，可以推导出对称视锥(常见的都是对称视锥，也符合人眼看物理的规律)的投影变换矩阵如下：

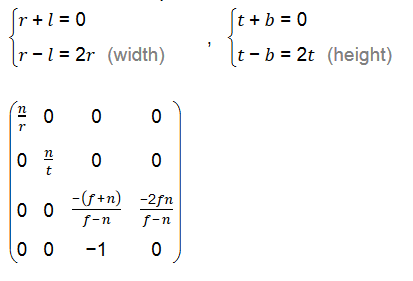
透视投影变换矩阵

其中，n为眼睛与近平面的距离(near)，f为眼睛与远平面的距离(far)，r为设备的宽度，t为设备的高度。

如何定义视界角度为alpha，定义设备的宽高比为 ar = width/height, 那么，投影矩阵也可以表述为：

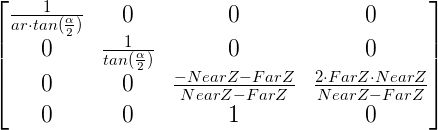
透视投影变换矩阵

对应的代码实现：

PipeLine & PipeLine::PerspectiveProject(float ar, float alpha, float znear, float zfar) {
    mat4x4f PrespectiveM = {
        1.0f/(tanf(alpha/2.0)*ar), 0.0f                  , 0.0f                      , 0.0f,
        0.0f                     , 1.0f/(tanf(alpha/2.0)), 0.0f                      , 0.0f,
        0.0f                     , 0.0f                  , (-znear-zfar)/(znear-zfar), (2*zfar*znear)/(znear-zfar),
        0.0f                     , 0.0f                  , 1.0f                      , 0.0f
    };
    mulmatf(PrespectiveM, M, M, 4, 4, 4);
    return *this;
}

投影变换对应的矩阵称为投影(projection)矩阵。

正交投影

构造正交投影(Orithographic Projection)的矩阵简单很多。所有的是眼坐标下xe, ye 和ze，都被线性的映射到NDC中。我们需要做的就是讲长方体视景体缩放为规范视见体，然后移动到原点。如下图所示：

正交投影

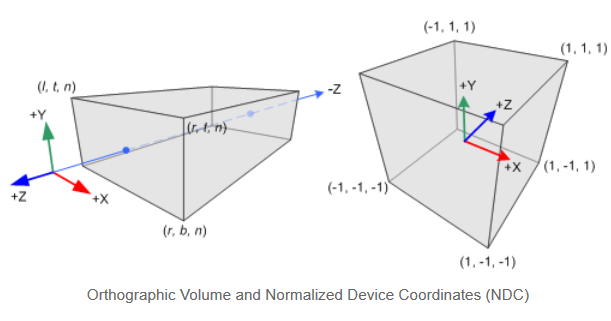
如果视锥是对称的话，投影矩阵为：

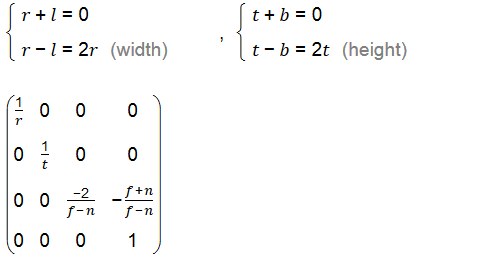
正交投影变换矩阵

相机空间

我们可以将相机放在三维空间的任意位置，然后将世界坐标系中的点转换到相机坐标系中，然后投影到设备屏幕上。理论上可以生成这样的变化矩阵，实现把一个位于3D空间的对象投影到坐落在世界坐标系任意位置的相机正前方的2D平面上。

三维相机的一个示意图：

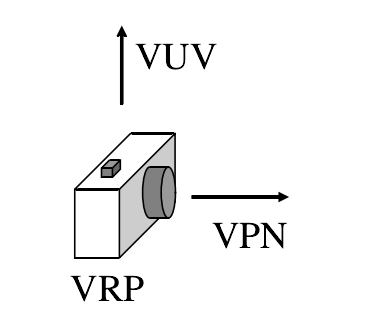
相机示意图

与UVN相关的概念包括:

相机位置，或者叫做视点(eyepoint): 观察参考点 (View Reference Point)
相机镜头方向，通过观察平面的法向量指定: 观察平面法向量VPN (View Plane Normal)
相机顶部正朝向: VUV (View Up Vector)

相机平移变换

移动相机是非常简单的。如果相机位于（x，y，z），那么平移变换就是（-x,-y,-y）。原因很明显——相机在世界坐标系下用向量（x,y,z）做平移变换，所以想要相机回到原点，那么我们就需要使用此向量的相反向量进行平移。变换矩阵如下所示：

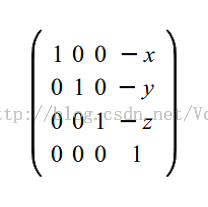
相机移动变换矩阵

相机旋转变换

下一步是将相机转向世界坐标系中指定的位置。我们想要找到在相机定义的新坐标系下顶点的位置。“UVN相机”是众多指定相机方向的办法中的一个。相机被下列的矩阵所定义：

N: 由相机指向它的目标的向量。在一些3D的文献中也被称为’look at’。这个向量对应于Z轴。
V: 直立时，这个向量相对于相机是竖直向上的。这个向量对应于Y轴。
U: 这个向量从相机指向其右侧。它对应于X轴。

为了把一个位置从世界坐标系空间转换到被UVN向量定义的相机坐标系空间，我们需要在位置和UVN向量之间进行一个点乘运算。我们可以把UVN系统看作是相机的基，从而可以方便的把一个向量在世界坐标和相机坐标进行转换(将世界坐标变换到相机坐标)。得到的相机旋转变换矩阵：

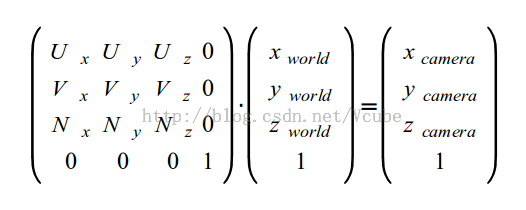
相机转动变换矩阵

下来讨论这个变换矩阵的推导过程。对于一个相机，我们容易知道它在三维坐标(世界坐标系)中的以下三个参数：

pos: 相机的位置坐标。
target: 相机正前方的目标点的坐标。
up: 相机的正上方(头顶)的方向向量。(一般为(0.0f, 1.0f, 0.0f)，与人平视屏幕时的头顶方向一致)。

根据这三个参数，注意到相机坐标系是右手坐标系，根据向量叉积的性质，容易求出：

N = norm(target - pos)
U = norm(up * N)
V = norm(N * U)

当相机在屏幕中定位时，它首先会进行朝向的确定——旋转，然后进行位置的确定——平移。因此，当进行相机变换的时候，将世界坐标系中的坐标变换到相机坐标系中的坐标时，应该进行一个相机定位的逆定位。先做逆平移变换，再做逆旋转变换。

关于相机变换矩阵的推导，参考了博文[推导相机变换矩阵][http://blog.csdn.net/popy007/article/details/5120158]。

相机变换对应的矩阵称为视图(view)矩阵，也称为观察矩阵。

数学运算库 glm 中包含了一个lookUp函数，可以根据pos, target和up三个向量来直接计算出相机变换矩阵：

glm::mat4 View = glm::lookAt(
    glm::vec3(4,3,3), // Camera is at (4,3,3), in World Space
    glm::vec3(0,0,0), // and looks at the origin
    glm::vec3(0,1,0)  // Head is up (set to 0,-1,0 to look upside-down)
);

摄像机控制

通过相机变换矩阵，我们可以利用矩阵乘法将世界坐标系中的坐标变换到相机坐标系中。通过修改pos, target 和 up 参数，我们可以在程序中动态完成相机的控制。但是这样仍然不能很好的用于人机交互，通常使用的第一人称相机，通过键盘WASD等键和鼠标来控制虚拟相机更加方便，因此需要改进我们的相机控制。要想构造适合人机交互的相机类，必须明确我们需要实现的目标。第一人称相机的目标包括:键盘来移动相机，是相机前后左右移动，通过鼠标来控制相机绕xy轴转动角度，通过鼠标滚轮来实现缩放。

第一人称相机旋转示意图：

第一人称相机旋转示意图图

可以将相机在空间的旋转、移动等变换都分解到 U、V、N 方向上进行，三个为了更好地表达对摄像机的控制，实现一个Camera类，代码实现：

// implements for class Camera
Camera::Camera(vec3f pos, vec3f target, vec3f up): POS(pos), TARGET(target), UP(up) {
    // initial camera.
    POS = pos; TARGET = target; UP = up;
    this->UpdateUVN();
}

Camera & Camera::Translate(float du, float dv, float dn) {
    vec3f delta(du*U.x + dv*V.x + dn*N.x, du*U.y + dv*V.y + dn*N.y, du*U.z + dv*V.z + dn*N.z);
    POS = POS + delta;
    TARGET = TARGET + delta;
    return this->UpdateUVN();
}

Camera & Camera::Rotate(float roll, float pitch, float yaw) {
    vec3f uu, vv, nn;

    uu = U, vv = V;
    U = uu * cosf(roll) - vv * sinf(roll);
    V = uu * sinf(roll) + vv * cosf(roll);

    vv = V, nn = N;
    V = vv * cosf(pitch) - nn * sinf(pitch);
    N = vv * sinf(pitch) + nn * cosf(pitch);

    // nn = N, uu = U;
    N = nn * cosf(yaw) - uu * sinf(yaw);
    U = nn * sinf(yaw) + uu * cosf(yaw);

    // update target and up.
    TARGET = POS + N; UP = V;

    return *this;
}

Camera & Camera::UpdateUVN() {
    // calculate the axis value of camera coordinate system.
    N = (TARGET - POS).Normalize();
    U = (UP * N).Normalize();
    V = (U * N).Normalize();
    return *this;
}

mat4x4f & Camera::TransformM() {
    memset(M, 0x00, sizeof(M));
    M[0][0] = M[1][1] = M[2][2] = M[3][3] = 1.0f;
    // calculate translation transform.
    mat4x4f TranslateM = {
        1.0f, 0.0f, 0.0f, -POS.x,
        0.0f, 1.0f, 0.0f, -POS.y,
        0.0f, 0.0f, 1.0f, -POS.z,
        0.0f, 0.0f, 0.0f, 1.0f
    };
    mulmatf(TranslateM, M, M, 4, 4, 4);
    // calculate rotation transform.
    mat4x4f RotateM = {
        U.x , U.y , U.z , 0.0f,
        V.x , V.y , V.z , 0.0f,
        N.x , N.y , N.z , 0.0f,
        0.0f, 0.0f, 0.0f, 1.0f
    };
    mulmatf(RotateM, M, M, 4, 4, 4);

    return this->M;
}

方向键控制六个方向上的移动：

static void SpecialKeys(int key, int, int)
{
    switch (key) {
    case GLUT_KEY_LEFT: camera.Translate(-STEP_VAL); break;
    case GLUT_KEY_RIGHT: camera.Translate(STEP_VAL); break;
    case GLUT_KEY_UP: camera.Translate(0.0f, STEP_VAL); break;
    case GLUT_KEY_DOWN: camera.Translate(0.0f, -STEP_VAL); break;
    case GLUT_KEY_PAGE_UP: camera.Translate(0.0f, 0.0f, STEP_VAL); break;
    case GLUT_KEY_PAGE_DOWN: camera.Translate(0.0f, 0.0f, -STEP_VAL); break;
    default: printf("Unknown Special Key: %d\n", key); break;
    }
}

鼠标拖拽：

glutMotionFunc(MotionFunc);
glutMouseFunc(MouseFunc);

static void MotionFunc(int x, int y)
{
    if(mstate) {
        camera.Rotate(0.0f, ToRadian((_y-y)*Camera::MOUSE_SENSITIVITY), ToRadian((_x-x)*Camera::MOUSE_SENSITIVITY));
        _x = x; _y = y; // update
    }
}

static void MouseFunc(int button, int state, int x, int y)
{
    if(button == GLUT_LEFT_BUTTON) {
        if(state == GLUT_DOWN) {
            _x = x, _y = y; mstate = true;
        }
        else {
            mstate = false;
        }
    }
}

MVP变换矩阵

M、V、P 分别指模型(model)，视图(view)和投影(projection)。MVP矩阵是模型、视图、以及投影变换三者结合起来的变换矩阵。变换顺序为：模型 -> 视图 -> 投影。变换方程表达：

MVP = model * view * projection

MVPTransform = model * view * projection * origin

在实际编程中，可以使用glm库来方便地实现这些操作：

    // Projection matrix : 45° Field of View, 4:3 ratio, display range : 0.1 unit <-> 100 units
    glm::mat4 Projection = glm::perspective(45.0f, 4.0f / 3.0f, 0.1f, 100.0f);
    // Camera matrix
    glm::mat4 View       = glm::lookAt(
        glm::vec3(4,3,3), // Camera is at (4,3,3), in World Space
        glm::vec3(0,0,0), // and looks at the origin
        glm::vec3(0,1,0)  // Head is up (set to 0,-1,0 to look upside-down)
    );
    // Model matrix : an identity matrix (model will be at the origin)
    glm::mat4 Model      = glm::mat4(1.0f);  // Changes for each model !
    // Our ModelViewProjection : multiplication of our 3 matrices
    glm::mat4 MVP        = Projection * View * Model; // Remember, matrix multiplication is the other way around

深度缓冲（Z-Buffer）

在OpenGL绘图过程中，我们会遇到这样的问题：一些理应被遮挡的面，因为绘制次序靠后，竟然变成可见的了。我们将用深度缓冲（Z-Buffer）算法解决它。

该问题的解决方案是：在缓冲中存储每个片段的深度（即“Z”值）；并且每次绘制片段之前要比较当前与先前片段的深度值，看谁离摄像机更近。

我们可以自己实现深度缓冲，但让硬件自动完成更简单：

// Enable depth test
glEnable(GL_DEPTH_TEST);
// Accept fragment if it closer to the camera than the former one
glDepthFunc(GL_LESS);

问题解决了。

透视投影

正交投影

相机空间

相机平移变换

相机旋转变换

摄像机控制

MVP变换矩阵

深度缓冲（Z-Buffer）

参考

Comments: