PageRank的MapReduce化以及SEO分析
摘要:PageRank是Google专有的算法,用于衡量特定网页相对于搜索引擎索引中的其他网页而言的重要程度。它由Larry Page和Sergey Brin在20世纪90年代后期发明。 PageRank实现了将链接价值概念作为排名因素。PageRank算法在搜索引擎领域占据着重要的地位,而在当今互联网规模不断扩大的时代背景下,借助MapReudce框架等技术 手段将PageRank算法并行化具有非常广泛的应用价值。同时,针对PageRank算法设计的SEO策略也对网站的发展有着重要的影响。本文将从PageRank算法的原理和背景出 发,分析算法的实现思路,尝试将PageRank算法MapReduce化,同时,简要从PageRank算法本身出发,讨论SEO和反SEO的思路。
关键词:搜索引擎, PageRank, MapReduce, SEO
一、概述
本文首先会讨论搜索引擎的核心难题,同时讨论早期搜索引擎关于结果页面重要性评价算法的困境,借此引出PageRank产生的背景。第二部分会详细讨论PageRank的思想来 源、基础框架,并结合互联网页面拓扑结构讨论PageRank处理Dead Ends及平滑化的方法。第三部分讨论PageRank算法MapReduce化的思路和具体实现。最后将讨论对 PageRank的SEO和反SEO的策略。
二、背景
从本质上说,搜索引擎是一个资料检索系统,搜索引擎拥有一个资料库(具体到这里就是互联网页面),用户提交一个检索条件(例如关键词),搜索引擎返回符合查询条件 的资料列表。我们知道Web页面数量非常巨大,所以一个检索的结果条目数量也非常多,一个好的搜索引擎必须想办法将“质量”较高的页面排在前面。直观上也可以感觉出, 在使用搜索引擎时,我们并不太关心页面是否够全,而很关心前一两页是否都是质量较高的页面,是否能满足我们的实际需求。
在PageRank提出之前,已经有研究者提出利用网页的入链数量来进行链接分析计算,这种入链方法假设一个网页的入链越多,则该网页越重要。早期的很多搜索引擎也采纳 了入链数量作为链接分析方法,对于搜索引擎效果提升也有较明显的效果。 PageRank除了考虑到入链数量的影响,还参考了网页质量因素,两者相结合获得了更好的网页 重要性评价标准。
PageRank算法在计算页面排名时基于以下两个假设:
- 数量假设:如果一个网页被很多其他网页链接到的话说明这个网页比较重要,也就是pagerank值会相对较高;
- 质量假设:如果一个pagerank值很高的网页链接到一个其他的网页,那么被链接到的网页的pagerank值会相应地因此而提高。
如下图中的节点的链接关系和PageRank权值便能很好地反映出这个问题:
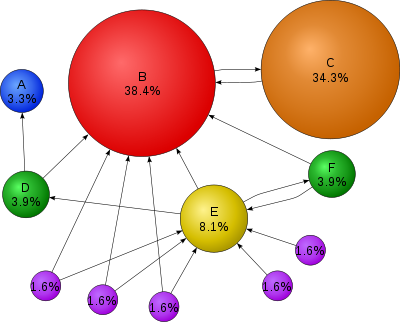
三、算法原理分析
PageRank算法的原理非常简单,假设一个由只有4个页面组成的集合:A,B,C和D,PR为其PageRank值,初始时,每个节点的 $PR$ 值都为 $1$,$L$ 为其外链数目,那么,以节点A为 例,其 $PR$ 值可由如下公式计算:
\[PR(A)= \frac{PR(B)}{L(B)}+ \frac{PR(C)}{L(C)}+ \frac{PR(D)}{L(D)}\]最后,所有这些被换算为一个百分比再乘上一个系数d。并将1-d的权值均匀加给每个节点,得到下式:
\[PR(A)=\left( \frac{PR(B)}{L(B)}+ \frac{PR(C)}{L(C)}+ \frac{PR(D)}{L(D)} \right) d + \frac{1 - d}{N}\]一个页面的PageRank是由其他页面的PageRank计算得到。如果给每个页面一个初始PageRank值(非0),那么经过不断的重复计算,这些页面的PR值会趋向于稳定,也就是 收敛的状态。
一般来说,\(d=0.85\)(这里的d被称为阻尼系数(damping factor),其意义是,在任意时刻,用户到达某页面后并继续向后浏览的概率。设置d值是为了为了处理那 些“没有向外链接的页面”(这些页面就像“黑洞”会吞噬掉用户继续向下浏览的概率)带来的问题,该数值是根据上网者使用浏览器书签的平均频率估算而得。
对于整个网络中的全部页面,每个页面的PageRank值可由下式表示:
\[PageRank(p_i) = \frac{1-d}{N} + d \sum_{p_j \in M(p_i)}^{}{\frac{PageRank(p_j)}{L(p_j)}}\]其中,$p_1, p_2, …, p_N$ 是被研究的页面,$M(p_i)$ 是链入 $p_i$ 页面的集合,$L(p_j)$ 是 $p_j$ 链出页面的数量,而 $N$ 是所有页面的数量。
四、幂法计算PageRank
PageRank值是一个特殊矩阵中的特征向量。这个特征向量为:
\[\mathbf{R} = \begin{bmatrix} PR(p_1) \\ PR(p_2) \\ \vdots \\ PR(p_N) \end{bmatrix}\]PageRank 公式可以转换为求解 \(\lim_{n \to \infty}{A^n X}\) 的值。 其中矩阵为
\[A=q \times P + (1 - q) * e e^t / N\]其中 $P$ 为概率转移矩阵,为 $n$ 维的全 $1$ 行列式。
幂法计算过程如下:
$X$ 设任意一个初始向量, 即设置初始每个网页的 PageRank 值,一般为$1$。
R = AX;
while(true)(
if (|X-R|<\eplison) { //如果最后两次的结果近似或者相同,返回R
return R;
}
else { // 否则继续迭代求解。
X = R;
R = A X;
}
}
Larry Page和Sergey Brin两人从理论上证明了不论初始值如何选取,这种算法都保证了网页排名的估计值能收敛到他们的真实值。同时,他们还利用稀疏矩阵计算的技巧, 大大的简化了计算量,使得网页数目的急剧增大不至于导致计算无法进行。
幂法计算PageRank的R代码实现:
#构建邻接矩阵
adjacencyMatrix<-function(pages){
n<-max(apply(pages,2,max))
A <- matrix(0,n,n)
for(i in 1:nrow(pages)) A[pages[i,]$dist,pages[i,]$src]<-1
A
}
#变换概率矩阵,考虑d的情况
dProbabilityMatrix<-function(G,d=0.85){
cs <- colSums(G)
cs[cs==0] <- 1
n <- nrow(G)
delta <- (1-d)/n
A <- matrix(delta,nrow(G),ncol(G))
for (i in 1:n) A[i,] <- A[i,] + d*G[i,]/cs
A
}
#直接计算矩阵特征值
calcEigenMatrix<-function(G){
x <- Re(eigen(G)$vectors[,1])
x/sum(x)
}
六、MapReduce化分析及实现
可以直接根据PageRank算法的简单公式:
\[Rv = alpha * Sigma(Rn/Nn)+ (1-apha)/N\]来实现并行化,大概思路为:
- Mapper 的输入格式为:(节点,PageRank 值)->(该节点的外部链接节点列表)
-
Mapper 的输出格式为:(节点) -> (该节点的反向链接节点,反向节点的 PankRank 值/反向节点的外链个数)
- Reducer 的输入格式(Mapper 的计算输出)为:(节点) -> (该节点的反向链接节点,反向节点的 PankRank 值/反向节点的外链个数)
- Reducer 的输出为:(节点, 新的 PageRank 值)
使用Python实现这一算法:
#! /usr/bin/env python
# -*- coding = utf-8 -*-
__author__ = 'He Tao, hetao@buaa.edu.cn'
class Node:
def __init__(self, id, pk):
self.id = id
self.pk = pk
def pk_map(map_input):
map_output = {}
for node, outlinks in map_input.items():
for link in outlinks:
size = len(outlinks)
if link in map_output:
map_output[link]+=(float)(node.pk)/size
else:
map_output[link]=(float)(node.pk)/size
return map_output
def pk_reduce(reduce_input):
for result in reduce_input:
for node,value in result.items():
node.pk += value
def pk_clear(nodes):
for node in nodes:
node.pk = 0
def pk_last(nodes):
lastnodes = []
for node in nodes:
lastnodes.append(Node(node.id,node.pk))
return lastnodes
def pk_diff(nodes,lastnodes):
diff=0
for i in range(len(nodes)):
print('node pk %f, last node pk %f ' % (nodes[i].pk, lastnodes[i].pk))
diff += abs(nodes[i].pk-lastnodes[i].pk)
return diff
def pk_test():
# Initial
node1 = Node(1, 0.25)
node2 = Node(2, 0.25)
node3 = Node(3, 0.25)
node4 = Node(4, 0.25)
nodes = [node1, node2, node3, node4]
threshold = 0.0001
max_iters = 100
for iter_count in range(max_iters):
iter_count += 1
lastnodes = pk_last(nodes)
print('============ map count %d =================' % (iter_count))
in1 = {node1: [node2, node3, node4], node2: [node3, node4]}
in2 = {node3: [node1, node4], node4: [node2]}
mapout1 = pk_map(in1)
mapout2 = pk_map(in2)
for node, value in mapout1.items():
print('%d %f'%(node.id, value))
for node, value in mapout2.items():
print('%d %f'%(node.id, value))
print('============ reduce count %d =================' % (iter_count))
reducein = [mapout1, mapout2]
pk_clear(nodes)
pk_reduce(reducein)
for node in nodes:
print('%d %f'%(node.id, node.pk))
diff = pk_diff(nodes,lastnodes)
if diff < threshold:
break
if __name__ == '__main__':
pk_test()
程序模拟的构图为:
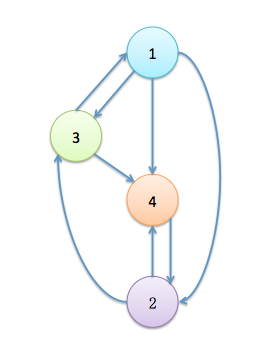
模拟有两个节点参与计算,初始时PageRank的值都为0.25,使用的阈值为0.0001,最多迭代的次数为100次。
程序仅仅迭代了15次就收敛到阈值,最终得到的结果为:
1 0.107138774577
2 0.35712924859
3 0.214296601128
4 0.321435375705
这个数值不仅与简单的PageRank实现得到的结果相同,并且从直观上看,这个结果也与这四个节点构成的网络图相对应。
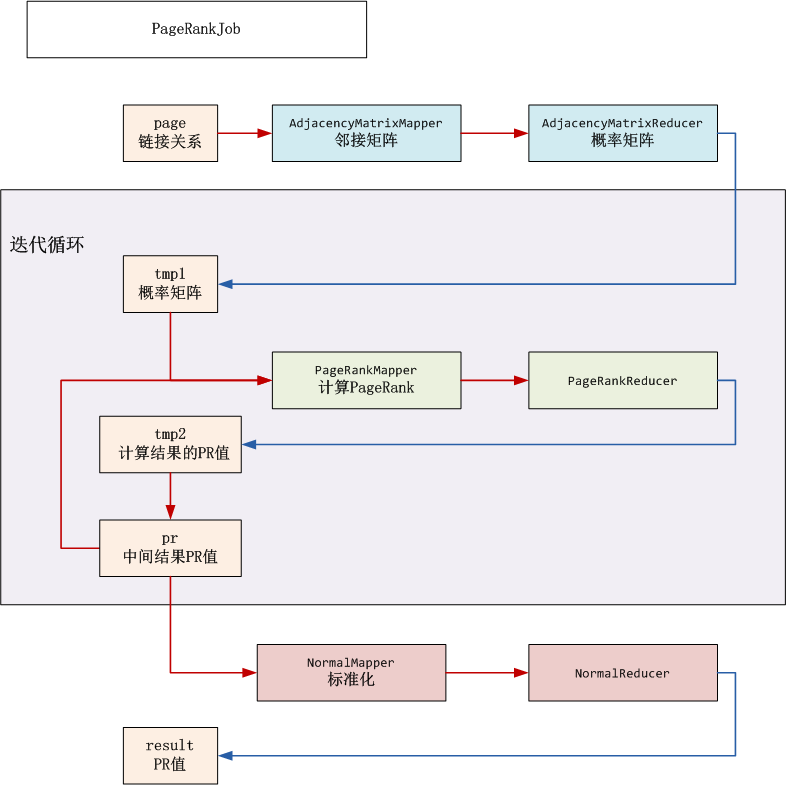
此外,将矩阵迭代并行化可以很好滴实现PageRank算法的并行化,其MapReduce流程分解如下图所示:
七、SEO以及反SEO
本文的最后,将结合前文中对PageRank算法的分析来讨论针对这一页面排名算法的SEO优化策略以及防范措施。
Google经常处罚恶意提高PageRank的行为,至于其如何区分正常的链接和不正常的链接仍然是个商业机密。但是在GOOGLE的链接方案(https://support.google.com/webmasters/answer/66356?hl=zh-Hans)中明确指出了那些行为将会受到惩罚。
如果一个搜索引擎仅仅依靠关键词的频率来确定页面的排名,那么一个网页将有能力影响一个关键词的搜索结果。例如,在个人博客页面中通过一个隐藏的div标签来重复“世界杯”十万次,当有用户搜索欧洲杯时,该博客页面就能出现在搜索结果较靠前的位置。这种行为就叫做“Term Spam”。而PageRank算法与早期的传统搜索引擎相比很好地解决了这个问题。
也有很多针对PageRank算法设计的Spam行为。PageRank主要靠内链数计算页面权重,并且,在PageRank算法中,一个页面会将权重均匀散播给被链接网站,所以除了内链数外,上游页面的权重也很重要。Spam PageRank的关键就在于想办法增加一些高权重页面的内链。首先,将页面分为以下四种类型:
- 目标页:目标页是spammer要提高rank的页面,这里就是个人博客首页。
- 支持页:支持页是spammer能完全控制的页面,例如spammer自己建立的站点中页面。
- 可达页:可达页是spammer无法完全控制,但是可以有接口供spammer发布链接的页面,例如天涯社区、知乎、新浪博客等等这种用户可发帖的社区或博客站。
- 不可达页:这是那些spammer完全无法发布链接的网站,例如政府网站、百度首页等等。
单纯通过支持页是没有办法spam的,因此需要尽量找一些rank较高的可达页去加上对个人博客首页的链接,例如在一些网络社区中发帖,帖文中贴出自己的链接。然后,再通过大量的支持页放大rank,具体做法是让每个支持页和目标页互链,且每个支持页只有一条链接。
下图就是这样一个Spam拓扑图:
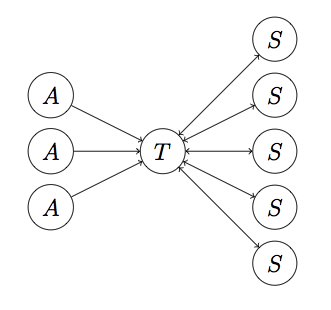
其中T是目标页,A是可达页,S是支持页。按照PageRank算法计算页面排名,最终的结果显示这个拓扑结构将会使得页面T的PageRank值放大约2.7倍!因此,这种策略在网页排名作弊中相当有效!
接下来,需要分析搜索引擎是如何防止这种Spam行为的。
一种方法是通过对网页的图拓扑结构分析找出可能存在的spam farm。但是随着Web规模越来越大,这种方法非常困难。
TrustRank放法是另一种可行的反作弊策略。TrustRank的思想很直观:如果一个页面的普通rank远高于可信网页的topic rank,则很可能这个页面被spam了。所谓可信网页例如政府网站、新浪、网易门户首页等等。
设一个页面普通rank为 $P$,TrustRank为 $T$,则定义网页的Spam Mass为:$\frac{P–T}{P}$。Spam Mass越大,说明此页面为spam目标页的可能性越大。
参考
- Wikipedia about PageRank
- Andreas Paepcke, Sriram Raghavan. Junghoo Cho Hector Garcia - Molina, Searching the Web
- S.Brin, L.Page. The Anatomy of a Large-scale Hypertextual Web Search Engine Computer Networks and ISDN Systems
- Lawrence Page, Sergey Brin, Rajeev Motwani, Terry Winograd. The PageRank Citation Ranking: Bringing Order to the Web, 1998
- PageRank算法并行实现, http://blog.fens.me/algorithm-pagerank-mapreduce/