几种求解PI的概率算法的探究和对比
$\pi$ 是一个重要的随机数,在数学研究中占有重要地位。求解PI的数值值也一直是数学研究的经典问题之一。本文将主要探讨几种求解PI的概率算法的原理和实现, 并对比其效率和准确度。
Mathematica中的 $\pi$
我们发现,在Mathematica中可以使用 $\pi$ 来做符号运算,很多运算都涉及到非常高深的数学知识,使用N[Pi, n]函数也能够求得 $\pi$ 的前 $n$ 位数值解。
那么为什么Mathematica能够以如此高的精度求解 $\pi$ 的值呢?
通过查阅Mathematica的文档,得知,Mathematica求解 $\pi$ 使用的是Chudnovsky公式,因其具有很好的收敛速度而在数值计算中被广泛采用。Chudnovsky 算法的表述如下:
\[\frac{1}{\pi} = 12\sum_{k=0}^{\infty} \frac{(-1)^k(6k)! (163\cdot 3344418k + 13591409)}{(3k)!(k!)^3(640320^3)^{k+1/2}}\]根据这个公式,可以编写如下Mathematica代码:
chud[n_] := N[1/(12*Sum[
((-1)^k*(6 k)!*(13591409 + 545140134 k))/
((3 k)!*(k!)^3*640320^(3 k + 3/2)),
{k, 0, n}], 5];
]);
运行如下命令:
chud[1] // N
将会输出
3.14159
可见,Chudnovsky算法确实具有非常好的收敛性能。
二、普通蒙特卡洛方法
普通蒙特卡洛(Monte Carlo)方法求解 $\pi$ 的值,是指每次随机产生一个在 $2\times 2$ 的正方形中的点,统计这个点在该正方形的内接圆里的概率 $p$。 圆周率 $\pi$ 的估计值为 $4p$。算法原理和实现都很简单,Mathematica代码如下(此处,仅仅统计在第一象限内的随机点的分布情况):
mc[n_] := Module[
{
in = 0,
total = 0
},
For[k=1,k<=n,k=k+1,
x=RandomReal[];
y=RandomReal[];
total=total+1;
If[x*x+y*y<=1,in=in+1]
];
N[in/total*4, 5]
];
重复运行1000000次随机:
Print[mc[1000000]];
得到如下的$\pi$的近似值的序列:
3.1432 3.1423 3.1399 3.1397 3.1429
可见,蒙特卡洛随机化算法的准确性还是比较高的。使用点落在圆内的概率来模拟 $\pi$ 的值也是很正确的选择。
三、随机数互质的概率
接下来采用另一种概率算法来计算 $\pi$ 的近似值。这个算法不同于之前的蒙特卡洛、蒲风投针等随机算法模型,也不同于通过迭代来计算 $\pi$ 的近似值的算法模型。
这一算法的依据是:两个随机正整数 $a, b$ 互质的概率为 $\frac{6}{\pi^2}$。这一性质的证明过程如下:
-
设两个数 $u,v$ 互质的概率为 $p$,则 $gcd(u,v)=d$ 当且仅当 $d u, d v$,$gcd(\frac{u}{d}, \frac{v}{d})=1$。 - 因此,任两个数最大公约数为 d 的概率为 $p/d/d$,即 $p/(d^2)$。
- 在正整数集合上有 \(p+p/4+p/9+ \dots +p/(n^2)+ \dots = 1\) 容易求得 \(p=\frac{6}{\pi^2}\)。
利用这一性质,只需要采取如下做法:
取一大整数 $N$,在 $1$ 到 $N$ 之间随机地取一对整数 $a, b$,找到它们的最大公约数 $(a,b)$,做 $n$ 次这样的实验,记录 $(a,b)=1$ 的情况次数 $m$, 计算出 $p=\frac{m}{n}$ 的值。便可以计算出 $\pi$ 的近似值。
该算法的Mathematica实现如下:
(* 此处采用本机Mathematica的Machine ID作为随机数的最大范围: *)
(* 6102-90797-51506 *)
primep[n_] := Module[
{
(* maximum range of random number. *)
machineid = 61029079751506,
is = 0,
total = 0
},
For[k =1, k <= n, k = k+1,
total = total + 1;
x = RandomInteger[{1, machineid}];
y = RandomInteger[{1, machineid}];
If[GCD[x,y]==1, is = is+1]
];
N[Sqrt[6/(is/total)], 5]
];
重复运行:
For[i=1,i<=5,i=i+1,Print[primep[1000000]]];
得到如下的结果序列:
3.1408 3.1407 3.1408 3.1398 3.1419
总的来看,结果的分布还是相当不错的,作为一个随机概率算法,有如此的准确性已经相当不容易了。
四、对比
画图分析 $\pi$,Chudnovsky算法,普通蒙特卡洛算法,整数互质概率算法这四种求解 $\pi$ 的数值值得结果:
n = 10;
pis = Table[N[Pi, 5], {k, 1, n}];
chuds = Table[chud[k], {k, 1, n}];
mcs = Table[mc[Prime[2^k]], {k, 1, n}];
primeps = Table[primep[Prime[2^k]], {k, 1, n}];
Print[pis];
Print[chuds];
Print[mcs];
Print[primeps];
ListLinePlot[{pis, chuds, mcs, primeps},
AxesOrigin -> {0, 0},
PlotRange -> {0, 4}
]
如下图所示:
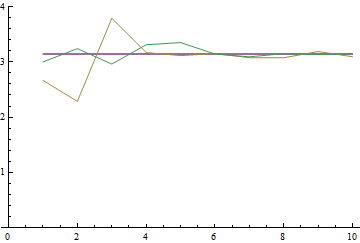
通过图像对比,不难看出Chudnovsky算法的高效和精确。在保留5位小数的情况下,Chudnovsky算法得到的结果和Mathematica自身算出来的结果已经重合,Chudnovsky算法仅仅做了一次迭代!
对比两种概率算法的结果,我们发现尽管是不同的概率模型,但由于其理论概率的保证,最终仍然都会收敛到 $\pi$ 的精确数值值。初期,由于基于整数互质概率的方法得到的结果偏离 实际情况过大,这也与随机整数的因数分布有关系,而当迭代次数增大时,这个方法得到的结果似乎要优于朴素蒙特卡洛方法的结果。这也启示我们,除了使用面积等古典概率 模型来进行数值模拟计算以外,数学上其他方面的一些理论成果也很有借鉴意义。
五、参考文献
六、附录:Mathematica代码
(* Chudnovsky algorithm*)
chud[n_] := N[1/(12*Sum[
((-1)^k*(6 k)!*(13591409 + 545140134 k))/
((3 k)!*(k!)^3*640320^(3 k + 3/2)),
{k, 0, n}], 5];
]);
(* Monte Carlo *)
mc[n_] := Module[
{
in = 0,
total = 0
},
For[k=1,k<=n,k=k+1,
x=RandomReal[];
y=RandomReal[];
total=total+1;
If[x*x+y*y<=1,in=in+1]
];
N[in/total*4, 5]
];
(* Prime model *)
primep[n_] := Module[
{
(* maximum range of random number. *)
machineid = 61029079751506,
is = 0,
total = 0
},
For[k =1, k <= n, k = k+1,
total = total + 1;
x = RandomInteger[{1, machineid}];
y = RandomInteger[{1, machineid}];
If[GCD[x,y]==1, is = is+1]
];
N[Sqrt[6/(is/total)], 5]
];
(* plot *)
n = 10;
pis = Table[N[Pi, 5], {k, 1, n}];
chuds = Table[chud[k], {k, 1, n}];
mcs = Table[mc[Prime[2^k]], {k, 1, n}];
primeps = Table[primep[Prime[2^k]], {k, 1, n}];
Print[pis];
Print[chuds];
Print[mcs];
Print[primeps];
ListLinePlot[{pis, chuds, mcs, primeps},
AxesOrigin -> {0, 0},
PlotRange -> {0, 4}
]