树状数组 | HE Tao

树状数组(Binary Index Tree, BIT)，是一个查询和修改复杂度都为O(lg(n))的数据结构。

定义

对于序列 $a$，我们设一个数组 $C$ 定义 $C[i] = a[i – 2^k + 1] + \dots + a[i]$ ($i$ 从 $1$ 开始)，$k$ 为 $i$ 在二进制下末尾 $0$ 的个数。 $k$ 的计算可以这样:

\[2^k = x \textit{ and } (x \textit{ xor } (x-1))\]

树状数组的结构如下图所示：

树状数组

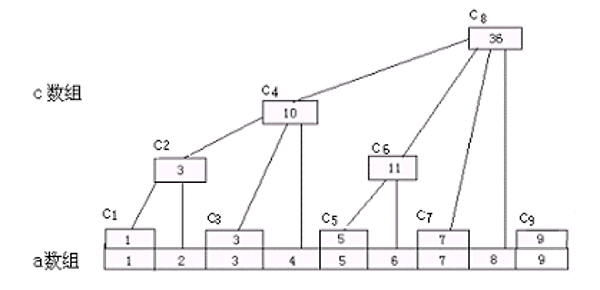
在实现时，可以定义宏

#define lowbit(x) ((x)&((x)^((x)-1)))

利用补码的特性，可以写为：

#define lowbit(x) ((x)&(-x))

来方便求得 $K$ 值。

建立树状数组

可以将数组中所有元素都初始化为 $0$，然后再逐个插入（修改）。

修改单个位置的值

/**
 * 将k位置的值增加delta。
 */
void change(int k, int delta)
{
    while(k <= n) {
        c[k] += delta;
        k += lowbit(k);
    }
}

查询区间和

首先，可以通过如下方法在 $O(\log{n})$ 的时间内得出前 $k$ 个元素的和。

/**
 * 求区间[1, k]内元素的和
 */
int query_sum(int k) {
    int _sum = 0;
    while(k > 0) {
        _sum += c[k];
        k -= lowbit(k);
    }
    return _sum;
}

区间和查询便不难实现：

/**
 * 求区间[x, y] 内元素的和。
 */
int query_range(int x, int y)
{
    return query_sum(y) - query_sum(x-1);
}

二维情形

直接将一维的所有操作扩展到二维即可。

更新：

/**
 * (x, y)处的值增加delta
 */
void change(int x, int y, int delta)
{
    while(x <= xn) {
        while(y <= yn) {
            c[x][y] += delta;
            y += lowbit(y);
        }
        x += lowbit(x);
    }
}

查询二维区间和操作：

/**
 * 查询(0,0)与(x, y)范围内的和。
 */
int query_sum(int x, int y) {
    int _sum = 0;
    while(x > 0) {
        while(y > 0) {
            _sum += c[x][y];
            y -= lowbit(y);
        }
        x -= lowbit(x);
    }
    return _sum;
}

/**
 * 查询(x1, y1)与(x2, y2)范围内的和
 */
int query_range(x1, y1, x2, y2) {
    return query_sum(x2, y2) + query_sum(x1-1, y1-1) -
            query_sum(x1-1, y2) - query_sum(x2, y1-1);
}

区间修改单点查询

线段树也可以用于区间修改单点值查询的场合。

在这种模型中，数组 $C$ 的含义有所不同。$c[i]$ 用来表示到目前为止 $a[1 \dots i]$ 共被整体加了多少。此时，$a[i]$ 的值为 $c[i \dots n]$ 之和。

对区间 $[x, y]$ 的修改可以变换为对区间 $[1, x]$ 和区间 $[1, y]$ 的修改。具体代码实现如下：

/**
 * 将[1, x]位置的值增加delta。
 */
void change(int k, int delta)
{
    while(k > 0) {
        c[k] += delta;
        k -= lowbit(k);
    }
}

/**
 * 将[x, y]区间的所有值增加delta
 */
void chang(int x, int y, int delta) {
    if(x > 1) {
        change(x-1, -delta);
    }
    change(y, delta);
}

/**
 * 求解原序列k处的值
 */
void query_value(int k) {
    int _value = 0;
    while(k <= n) {
        _value += c[i];
        k += lowbit(k);
    }
    return _value;
}

这样的区间修改单点查询的模型同样可以用于多维情形。

区间修改区间查询

这种情形需要两个辅助数组。$c[i]$ 用来记录 $a[1 \dots n]$ 共被整体加了多少次，$d[i]$ 用来记录 $a[1 \dots n]$ 到目前为止共被整体加了多少的总和。也即 $d[i] = a[i] \times i$。

代码实现如下：

void change_c(int k, int delta) { // change c[].
    while(k > 0) {
        c[k] += delta;
        k -= lowbit(k);
    }
}

void change_d(int k, int delta) { // change d[].
    int tmp = k;
    while(k <= n) {
        d[k] += tmp * delta; // 总和
        k += lowbit(k);
    }
}

void sum_c(int k) {
    int _sum = 0;
    while(k <= n) {
        _sum += c[k];
        k += lowbit(k);
    }
    return _sum;
}

void sum_d(int k) {
    int _sum = 0;
    while(k > 0) {
        _sum += d[k];
        k -= lowbit(k);
    }
    return _sum;
}

void change(int x, int y, int delta) {
    change_c(y, delta); change_d(y, delta);
    if(x > 1) {
        change_c(x-1, -delta); change_d(x-1, -delta);
    }
}

void query_sum(int k) {
    if(k) {
        return sum_c(k)*k + sum_d(k-1);
    }
    else {
        return 0;
    }
}

void query_range(int x, int y) {
    return query_sum(y)-query_sum(x-1);
}

与线段树的对比

优势

相对于使用线段树进行区间和动态查询，树状数组有如下优势：

空间复杂度降低；
编程复杂度降低；
无递归操作，栈空间占用小；
在时间复杂度上，相对于线段树常数要小一些。

局限

能用树状数组实现的，都能用线段树实现，反之并不成立。

参考

树状数组，百度百科

定义