一类棋盘覆盖问题的动态规划求解
棋盘覆盖问题是算法研究和实践中一个很有意思的问题。在解决这一类问题时,往往需要用到动态规划、状态压缩、二进制拆分、快速幂等多种算法技巧。
1x2 - 2xn
首先考虑一个较为简单的问题,使用1x2的骨牌覆盖2xn的棋盘,问:有多少种方案。
分析,注意到骨牌面积(1x2)和棋盘面积(2xn)之间的关系,只有以下两种放置方法:
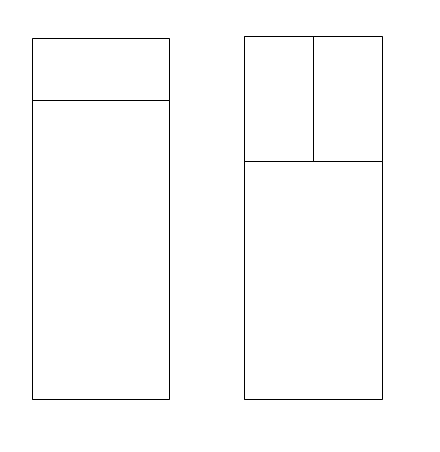
显然,不难得到这样的结论:
\[f(n) = f(n-1) + f(n-2)\]这便是Fibonacci数列的递推公式。
1x2 - 3xn
下来我们考虑使用1x2的骨牌覆盖3xn的棋盘的问题。根据上一题中我们的经验不难想到可以从上一行的状态来推出当前行的状态,从而根据状态转移和状态量来得到最终解的个数。对于3xn的棋盘,我们应该怎样处理呢?
当有三列时,当第i-1行摆好后,第i行可能会出现如下图所示的八种状态:
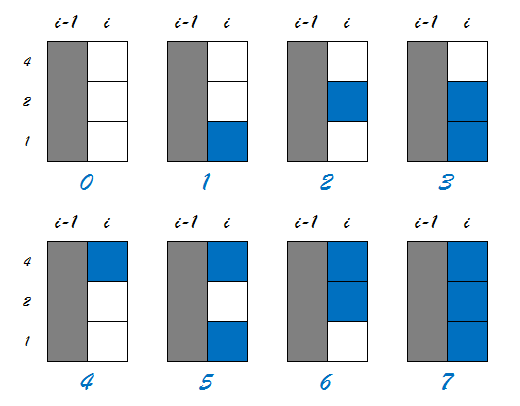
考虑这八种状态有分别会如下影响下一行的状态,拿状态 1 举例,当出现状态 1 的局面时,有以下两种放法:
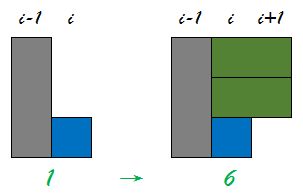
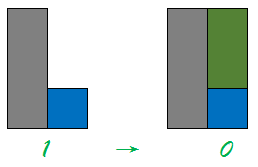
对于第一种方案,对于第i行状态1,我们在第i+1行竖放两块骨牌之后便能到达状态6。对于第二种方案,相当于第i行的状态1变成了第i行的状态7,本质上并没有改变 第i+1行的状态,而对于第i行的状态7,不做任何动作便能够转移到第i+1行的状态0。通过枚举八种状态的转移,可以得到如下图所示的状态转移矩阵:
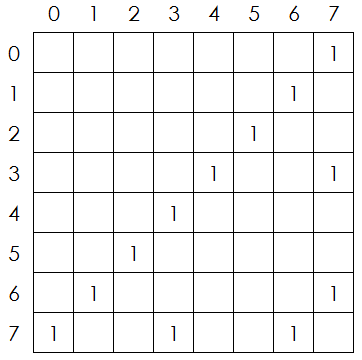
其中,第i行第j列的位置的值表示两行之间从状态i变为状态j的方案数。之后,便可以通过矩阵乘法来递推最后一行的状态的方案数了。而由于第0行的状态肯定是7, 因此,初始状态向量为(0, 0, 0, 0, 0, 0, 1)。最终只用统计第n行状态为7的方案数即可。
对于3xn的情况,还有另外一种思考方式:
n为奇数肯定为0,n为偶数,每次都是加两列,我们把两列看为一列,如果这一列与前面分开就只有三种方法即3*a[n-2],如果这一列不与前面的分开,那么不可分
解矩形都只有两种情况所以为2*(a[n-4]+a[n-6]+...+a[0])。化简即为a[n]=4*a[n-2]-a[n-4]。
1x2 - kxn
考虑更加普适性的问题,如果要覆盖一个kxn的棋盘,又应该如何去推导状态转移矩阵呢?
假设当第i行的状态为x,第i-1行的状态为y,那么有如下三种放置策略:
- 第i行不放置,则前一行必须有放置的骨牌。x对应二进制位为0,y对应二进制位为1。
- 第i行竖放骨牌,则前一行必须为空。x对应二进制位为1,y对应二进制位为0。
- 第i行横向骨牌,则前一行必须两个位置均有骨牌,否则会产生空位。x对应二进制位为1,y对应二进制位为1。
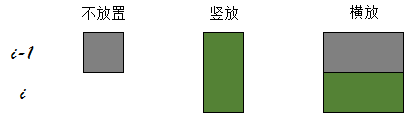
这三种策略分别对应一下三种状态转移:
- 第i行不放置:
new_x = x << 1,new_y = (y << 1) + 1; 列数+1 - 第i行竖放骨牌:
new_x = (x << 1) + 1,new_y = y << 1; 列数+1 - 第i行横向骨牌:
new x = (x << 2) + 3,new_y = (y << 2) + 3; 列数+2
根据上述分析,只需要进行dfs便可以找到状态转移矩阵:
int n, k, mat[1<<7][1<<7];
void dfs(int column, int now, int pre) {
if(column > k) { return; }
if(column == k) { mat[pre][now]++; return; }
dfs(column+1, (now<<1), (pre<<1)|1);
dfs(column+1, (now<<1)|1, (pre<<1));
dfs(column+2, (now<<2)|3, (pre<<2)|3);
}
当k较大时,便无法使用状态转移矩阵乘法的方法来解决问题,此时,需要存下状态转移矩阵中所有的边,然后递推。例如POJ 2411: Mondriaan’s Dream。 对应的DFS过程改成:
const int maxh = 11, maxw = 11;
int h, w, edge[(1<<maxw)*maxw+1][2], top = 0;
void dfs(int l, int now, int pre) {
if(l > w) { return; }
if(l == w) { edge[top][0] = pre; edge[top++][1] = now; return; }
dfs(l+1, now<<1, (pre<<1)|1);
dfs(l+1, (now<<1)|1, pre<<1);
dfs(l+2, (now<<2)|3, (pre<<2)|3);
}
此处应当注意存边的二维数组的体积:(1<<maxw)*maxw。
然后就是简单的递推了:
long long dp[maxh+1][1<<maxw] = 0;
dp[0][(1<<w)-1] = 1;
for(int i = 0; i < h; ++i) {
for(int j = 0; j < top; ++j) {
dp[i+1][edge[j][1]] += dp[i][edge[j][0]];
}
}
return dp[h%2][(1<<w)-1];
还可以进一步压缩空间:
long long dp[2][1<<maxw] = 0;
dp[0][(1<<w)-1] = 1;
for(int i = 0; i < h; ++i) {
memset(dp[(i+1)%2], 0x00, sizeof(dp[0][0])*(1<<maxw));
for(int j = 0; j < top; ++j) {
dp[(i+1)%2][edge[j][1]] += dp[i%2][edge[j][0]];
}
}
return dp[h%2][(1<<w)-1];