N皇后问题
N皇后问题是一个经典的问题,在一个N*N的棋盘上放置N个皇后,每行一个并使其不能互相攻击(同一行、同一列、同一斜线上的皇后都会自动攻击)。N皇后问题互 不相同的解的个数可以用OEIS A000170序列来表示,如果将旋转和对称的解归为一种,那么独立解的个数符合序列OEIS A002562。
普通递归求解
N皇后问题的普通解法是通过枚举N的全排列,并判断是否符合条件来得到解的方案数。可以通过一些剪枝技巧来优化运算,提升效率。
位运算求解
使用位运算可以显著提升运算效率。这是目前公认N皇后的最高效算法:
// 试探算法从最右边的列开始。
void nqueens(long row, long ld, long rd) {
if(row != upperlim) {
// row,ld,rd进行“或”运算,求得所有可以放置皇后的列,对应位为0,
// 然后再取反后“与”上全1的数,来求得当前所有可以放置皇后的位置,对应列
// 改为1
// 也就是求取当前哪些列可以放置皇后
long pos = upperlim & ~(row | ld | rd);
while(pos) { // 0 -- 皇后没有地方可放,回溯
// 拷贝pos最右边为1的bit,其余bit置0
// 也就是取得可以放皇后的最右边的列
long p = pos & -pos; // pos & (~pos+1);
// 将pos最右边为1的bit清零
// 也就是为获取下一次的最右可用列使用做准备,
// 程序将来会回溯到这个位置继续试探
pos -= p;
// row + p,将当前列置1,表示记录这次皇后放置的列。
// (ld + p) << 1,标记当前皇后左边相邻的列不允许下一个皇后放置。
// (ld + p) >> 1,标记当前皇后右边相邻的列不允许下一个皇后放置。
// 此处的移位操作实际上是记录对角线上的限制,只是因为问题都化归
// 到一行网格上来解决,所以表示为列的限制就可以了。显然,随着移位
// 在每次选择列之前进行,原来NxN网格中某个已放置的皇后针对其对角线
// 上产生的限制都被记录下来了
nqueens(row + p, (ld + p) << 1, (rd + p) >> 1);
}
}
else {
// row的所有位都为1,即找到了一个成功的布局,回溯
sum++;
}
}
- 初始化:
upperlim = (1<<n)-1; sum = 0; - 调用参数:
nqueens(0, 0, 0); - 结果:
sum
分析:这是一个递归函数,程序一行一行地寻找可以放皇后的地方。函数带三个参数row、ld和rd,分别表示在纵列和两个对角线方向的限制条件下这一行的哪些地方
不能放。位于该行上的冲突位置就用row、ld和rd中的1来表示。把它们三个并起来,得到该行所有的禁位,取反后就得到所有可以放的位置(用pos来表示)。
p = pos & (~pos + 1)其结果是取出最右边的那个1。这样,p就表示该行的某个可以放子的位置,把它从pos中移除并递归调用nqueens过程。
注意递归调用时三个参数的变化,每个参数都加上了一个禁位,但两个对角线方向的禁位对下一行的影响需要平移一位。最后,如果递归到某个时候发现row=upperlim了,
说明n个皇后全放进去了,找到的解的个数加1。如下图所示:
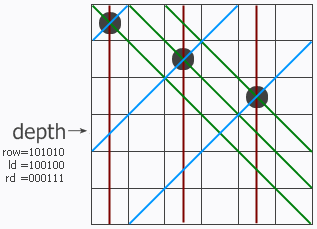
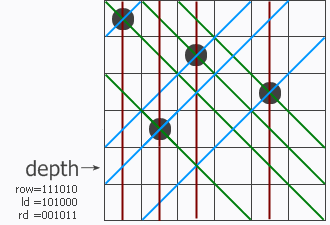
upperlime = (1 << n) - 1: 生成了n个1组成的二进制数。
(ld | p) << 1是因为由ld造成的占位在下一行要右移一下; (rd | p) >> 1是因为由rd造成的占位在下一行要左移一下。
ld rd row还要和upperlime与运算 一下,这样做的结果就是从最低位数起取n个数为有效位置,原因是在上一次的运算中ld发生了右移,如果不and的话,就会
误把n以外的位置当做有效位。
在进行到某一层的搜索时,pos中存储了所有的可放位置,为了求出所有解,必须遍历所有可放的位置,而每走过一个点必须要删掉它,否则就成死循环。
巧妙之处在于:以前我们需要在一个N*N正方形的网格中挪动皇后来进行试探回溯,每走一步都要观察和记录一个格子前后左右对角线上格子的信息;采用bit位进行信息存储 的话,就可以只在一行格子也就是(1行×N列)个格子中进行试探回溯即可,对角线上的限制被化归为列上的限制。
程序中主要需要下面三个bit数组,每位对应网格的一列,在C中就是取一个整形数的某部分连续位即可。row用来记录当前哪些列上的位置不可用,也就是哪些列被皇后占
用,对应为1。ld,rd同样也是记录当前哪些列位置不可用,但是不表示被皇后占用,而是表示会被已有皇后在对角线上吃掉的位置。这三个位数组进行“或”操作后就是表示当前还有哪些位置可以放置新的皇后,对应0的位置可放新的皇后。
所有下一个位置的试探过程都是通过位操作来实现的。
完整实现
/**
* N Queens Problem
* 试探-回溯算法,递归实现
*/
#include <iostream>
#include <ctime>
using namespace std;
// sum用来记录皇后放置成功的不同布局数;upperlim用来标记所有列都已经放置好了皇后。
long sum = 0, upperlim = 1;
void nqueens(int row, int ld, int rd) {
int pos, p;
if(row != upperlim) {
pos = upperlim & (~(row | ld | rd ));
while(pos){
p = pos & (~pos + 1);
pos = pos - p;
nqueens(row | p, (ld | p) << 1, (rd | p) >> 1);
}
}
else {
++sum;
}
}
int main(int argc, char *argv[])
{
time_t tm;
int n = 16;
if (argc != 1)
n = atoi(argv[1]);
tm = time(0);
// 因为整型数的限制,最大只能32位,
// 如果想处理N大于32的皇后问题,需要
// 用bitset数据结构进行存储
if ((n < 1) || (n > 32)) {
exit(-1); // 只能计算1-32之间
}
printf("%d 皇后\n", n);
// N个皇后只需N位存储,N列中某列有皇后则对应bit置1。
upperlim = (upperlim << n) - 1;
nqueens(0, 0, 0);
printf("共有%ld种排列, 计算时间%d秒 \n", sum, (int) (time(0) - tm));
return 0;
}
方案构造
除了求解解的个数以外,求解一个摆放方案也是一个极具挑战性的问题。对于N皇后问题,有如下结论:
一、当n mod 6 != 2 && n mod 6 != 3时:
[2,4,6,8,...,n],[1,3,5,7,...,n-1] (n为偶数)
[2,4,6,8,...,n-1],[1,3,5,7,...,n] (n为奇数)
二、当n mod 6 == 2 或 n mod 6 == 3时
设变量k,当n为偶数,k=n/2; 当n为奇数,k=(n-1)/2:
(k为偶数,n为偶数)
[k,k+2,k+4,...,n],[2,4,...,k-2],[k+3,k+5,...,n-1],[1,3,5,...,k+1]
(k为偶数,n为奇数)
[k,k+2,k+4,...,n-1],[2,4,...,k-2],[k+3,k+5,...,n-2],[1,3,5,...,k+1],[n]
(k为奇数,n为偶数)
[k,k+2,k+4,...,n-1],[1,3,5,...,k-2],[k+3,...,n],[2,4,...,k+1]
(k为奇数,n为奇数)
[k,k+2,k+4,...,n-2],[1,3,5,...,k-2],[k+3,...,n-1],[2,4,...,k+1],[n ]
上式中,方括号[]仅仅用来表示解的子序列特征。
例题:POJ 3239: Solution to the n Queens Puzzle
按照上述结论,容易得到题解:
#include <iostream>
#include <cstdio>
using namespace std;
void queens_puzzle(int n) { // n>=8
if(n%6!=2 && n%6!=3) {
printf("2");
for(int i=4;i<=n;i+=2)
printf(" %d",i);
for(int i=1;i<=n;i+=2)
printf(" %d",i);
printf("\n");
}
else {
int k=n/2;
if(n%2==0 && k%2==0) {
printf("%d",k);
for(int i=k+2;i<=n;i+=2)
printf(" %d",i);
for(int i=2;i<=k-2;i+=2)
printf(" %d",i);
for(int i=k+3;i<=n-1;i+=2)
printf(" %d",i);
for(int i=1;i<=k+1;i+=2)
printf(" %d",i);
}
else if(n%2==1 && k%2==0) {
printf("%d",k);
for(int i=k+2;i<=n-1;i+=2)
printf(" %d",i);
for(int i=2;i<=k-2;i+=2)
printf(" %d",i);
for(int i=k+3;i<=n-2;i+=2)
printf(" %d",i);
for(int i=1;i<=k+1;i+=2)
printf(" %d",i);
printf(" %d",n);
}
else if(n%2==0 && k%2==1) {
printf("%d",k);
for(int i=k+2;i<=n-1;i+=2)
printf(" %d",i);
for(int i=1;i<=k-2;i+=2)
printf(" %d",i);
for(int i=k+3;i<=n;i+=2)
printf(" %d",i);
for(int i=2;i<=k+1;i+=2)
printf(" %d",i);
}
else {
printf("%d",k);
for(int i=k+2;i<=n-2;i+=2)
printf(" %d",i);
for(int i=1;i<=k-2;i+=2)
printf(" %d",i);
for(int i=k+3;i<=n-1;i+=2)
printf(" %d",i);
for(int i=2;i<=k+1;i+=2)
printf(" %d",i);
printf(" %d",n);
}
printf("\n");
}
}
int main(int argc, char **argv) {
int n;
while(~scanf("%d",&n)) {
if(!n) break;
queens_puzzle(n);
}
return 0;
}