The Einstein summation convention, introduced by Albert Einstein, is a notational convention that represents summation over a set of indexed term in a formula, achieving notational brevity. With Einstein summation convention, many common linear algebraic operations on multi-dimensional arrays can be represented in a simple fashion.

einsum

numpy.einsum implements the evaluation of Einstein summation convention. The subscripts string is a common-separated list of subscript labels, where each label refers to a dimension of the corresponding operand. When a label is repeated, it is summed. The rules of numpy.einsum can be summarized as1:

  1. Repeating subscript between input arrays means that values along those axes will be multiplied. The products make up the values for the output array.
  2. Omitting a latter from the output means values along that axis will be summed.
  3. We can return the unsummed axes in any order (specified by the output subscripts).

In implicit mode (without output subscript labels), the axes of output are reordered alphabetically according to the chosen subscripts. In explicit mode (with output subscript labels), the output can be directly controlled by specifying output subscript labels. For example, in implicit mode, ij,jk returns the matrix multiplication of input operands, however ij,jh returns the transpose of matrix multiplication, because h precedes i in alphabet. In explicit mode, the output axes order can be directly specified as ij,jh->ih.

>>> a = np.array(range(0, 4)).reshape(2, 2)
>>> b = np.array(range(0, 6)).reshape(2, 3)
>>> np.einsum("ij,jk", a, b)
array([[ 3,  4,  5],
       [ 9, 14, 19]])

>>> np.einsum("ij,jh", a, b)
array([[ 3,  9],
       [ 4, 14],
       [ 5, 19]])

>>> np.einsum("ij,jh->ih", a, b)
array([[ 3,  4,  5],
       [ 9, 14, 19]])

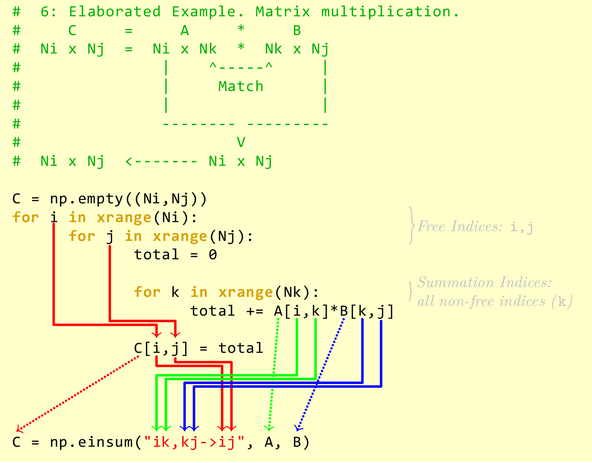
All indices in an Einstein summation can be partitioned into two sets:

  • free indices: used in the output specification, associated with the outer for-loop.
  • summation indices: used to compute and sum over the product terms, associated with the inner for-loop.

The basic idea can be elaborated with the following example2:

Matrix Multiplication with `einsum`

The numpy-style broadcasting is supported by using ..., or Ellipsis. For example,

  • i...i means take the trace along the first and last dimensions.
  • ...ii->...i means take the diagonal of the last two dimensions.
  • ij...,jk...->ik... returns a matrix multiplication with the left-most indices instead of the right-most indices.

When there is only one operand, no axes are summed, and no output parameter is provided, a view into operand is returned, instead of returning a new array. When the input array is mutable (writable), the result view is also mutable (writable). For example,

>>> a = np.array(range(9)).reshape(3, 3)
>>> np.einsum("ii->i", a)[:] = -1
>>> a
array([[-1,  1,  2],
       [ 3, -1,  5],
       [ 6,  7, -1]])

The einsum can be used to implemented many common linear algebraic operators on multi-dimensional arrays34:

  • np.trace: ii or ii->

    The i is repeated, thus will be summed.

  • np.diag: ii->i

    The i is repeated, but also occurs in output, thus won’t be summed.

  • np.sum(axis=1): ij->i

    The i is repeated (in input and output) and j isn’t, thus the i axes will be summed.

  • np.sum(axis=k): ...j...->...

    Sum over a single index for high-dimensional arrays.

  • np.transpose: ji or ij->ji

  • np.inner: i,i

  • Matrix-vector multiplication: ij,j

  • Matrix-matrix multiplication: ij,jk or ij,jk->ik

  • Vector outer product: i,j

einsum_path

numpy.einsum_path evaluates the lowest cost contraction order for a given Einstein summation notation, by considering the creation of intermediate arrays. The result of einsum_path is the order of input contraction, and can be used by einsum repeatedly later to evaluate the expression, without computing the optimization plan repeatedly.

>>> a = np.ones(64).reshape(2, 4, 8)
>>> path = np.einsum_path('ijk,ilm,njm,nlk,abc->', a, a, a, a, a, optimize='optimal')
>>> print(path[0])
['einsum_path', (0, 3), (0, 1), (1, 2), (0, 1)]
>>> print(path[1])
  Complete contraction:  ijk,ilm,njm,nlk,abc->
         Naive scaling:  9
     Optimized scaling:  5
      Naive FLOP count:  1.311e+06
  Optimized FLOP count:  2.305e+03
   Theoretical speedup:  568.642
  Largest intermediate:  6.400e+01 elements
--------------------------------------------------------------------------
scaling                  current                                remaining
--------------------------------------------------------------------------
   5               nlk,ijk->injl                       ilm,njm,abc,injl->
   5               njm,ilm->injl                          abc,injl,injl->
   4                 injl,injl->                                   abc,->
   3                      ,abc->                                       ->
>>> np.einsum('ijk,ilm,njm,nlk,abc->', a, a, a, a, a, optimize=path[0])
262144.0

References

  1. A basic introduction to NumPy’s einsum ↩

  2. Einstein Summation in Numpy ↩

  3. Numpy documentation for einsum ↩

  4. Einsum Is All You Need – Einstein Summation in Deep Learning ↩