K-近邻算法(KNN)
K-近邻算法(KNN, K Nearest Neighbors)是最基本、最简单、最有效的分类算法之一。KNN算法精度高、对异常值不敏感,可以有效地处理数据缺失的情况,但同时,KNN 算法的计算时间复杂度和空间复杂度都很高,特别是运行时需要载入全部数据,会占用很大的内存空间。
KNN算法的基本原理:输入未分类的(没有标签的)新数据时,将新数据的每个特征与样本集中的数据所对应的特征进行比较,然后提取出最相似的分类,作为新数据的分类。 一般来说,选取样本集中最相似的前 $k$ 个元素作为分类标准。通常来说,$k$ 的值不大于20,选择这 $k$ 个最相似元素中出现次数最多的分类作为新数据的分类。
kNN算法的一般步骤
-
准备数据
导入数据集,格式化数据。在这个过程中,有时需要补全数据缺失项和做规格化数据的预处理。
-
分析数据
通过图标、相关性分析等方法选择出数据集与分类相关的特征值,将其作为KNN分类的基础。
-
计算距离,分类
通过与样本集比较,对测试集分类,有时,也可以用作预测。
准备数据
很多时候,数据的某些特征与分类无关,如果将这些特征应用于KNN算法,可能会影响到分类的准确性,因此,需要先对数据进行分析,去除无关特征。
如下例所示,通过散点图的方法,不难看出以下样本集中,不同特征对分类的影响是不同的。
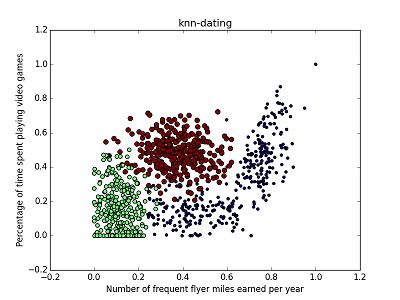
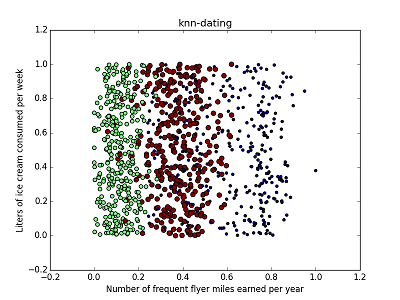
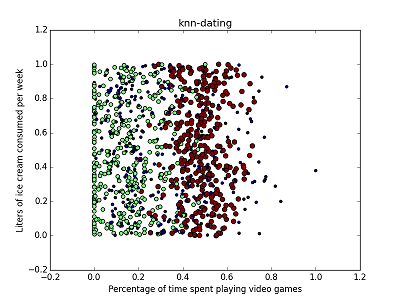
可见,选取不同的特征作为x,y轴时,数据集中各类的点分布是不同的。在数据分析阶段,除了以上使用的散点图,还可以使用相关性分析等方法进行数据特征分析。
距离的计算
通常,直接采用特征向量的几何距离作为数据之间的距离。
在计算距离时必须考虑到数据规一化的问题。由于数据的不同特征的值相差太大,如果不做规一化处理,很可能会导致最终距离仅仅能够反映特征向量某一分量的特点。 因此,必须根据特征的重要性等来对数据进行规一化预处理。
比如,以下数据集如果不做规格化处理,KNN算法分类的结果会很不准确。
42666 13.276369 0.543880 largeDoses
67497 8.631577 0.749278 didntLike
35483 12.273169 1.508053 largeDoses
50242 3.723498 0.831917 didntLike
63275 8.385879 1.669485 didntLike
一般来说,规一化数据的方法为依据特征值将数据值变换到 $0-1$ 或者 $-1-1$之间。可以通过以下公式进行:
\[new_val = \frac{old_val-min}{max-min}\]此公式可以把数据规格化到 $0-1$ 之间。
在归一化处理时,还可以根据之前的分析,对不同的特征分量加上不同的权重,以提高分类的准确率。
附件
- knn-dating, 测试用数据:dating.zip。
- KNN 手写数字识别, 测试用数据:handwriting.zip。
参考
- 机器学习实战(Machine Learning in Action)