斐波那契数列

2014年蓝桥杯本科C/C++组预赛第9题是很好的一道关于斐波那契(Fibonacci)数列的题目。本文将从这一题目出发，探讨一些与斐波那契数列相关的性质。

题目

题目链接：斐波那契 http://lx.lanqiao.org/problem.page?gpid=T121

题目内容：

问题描述

斐波那契数列大家都非常熟悉。它的定义是：

\[f(x) = {\begin{cases} 1 & x = 1, 2 \\ f(x-1) + f(x-2) & x > 2 \end{cases}}\]

对于给定的整数 $n$ 和 $m$，我们希望求出：$f(1) + f(2) + \dots + f(n)$ 的值。但这个值可能非常大，所以我们把它对 $f(m)$ 取模。

公式如下:

\[(\sum_{i=1}^n{f(i)}) \textit{ mod } f(m)\]

但这个数字依然很大，所以需要再对 $p$ 取模。

输入格式输入为一行用空格分开的整数 n m p ($0 < n, m, p < 10^{18}$)

输出格式输出为1个整数，表示答案

样例输入 2 3 5

样例输出 0

样例输入 15 11 29

样例输出 25

Fibonacci数列

通过递推式和特征方程，不难得到Fibonacci数列的通项公式为：

\[f(n)={\frac{1}{\sqrt{5}}}((\frac{1+\sqrt(5)}{2})^n-(\frac{1+\sqrt(5)}{2})^n)\]

根据Fibonacci数列的递推关系，可以使用矩阵乘法的方法来在O(log n)的时间复杂度内求得Fibonacci数列的第 n 项的值。具体算法：

\[A=\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}, f(n)=A^{n-1}[0][0]\]

Fibonacci数列有很多很有用的性质，首先根据Fibonacci数列的递推关系，有：

\[f(n+1) = f(n) + f(n-1)\]

那么，由此得到：

\[f(n) = f(n+1)-f(n-1)\]

从这个等式可以推出：

\[\begin{aligned} \sum_{i=1}^n {f(i)} &= f(1)+f(2)+f(3)+\dots+f(n) \\ &= f(1)+f(3)-f(1)+f(4)-f(2)+\dots+f(n+1)-f(n-1) \\ &= f(n)+f(n+1)-f(2) \\ &= f(n+2)-1 \end{aligned}\]

这个性质非常重要，通过这个性质，可以将Fibonacci数列前 $N$ 项的求和转化为求解某一项的值。

与上式同理，不难得到：

\[\begin{aligned} \sum_{i=1}^n {f(2*i-1)} &= f(1)+f(3)+f(5)+\dots+f(2*n-1) \\ &= f(2*n)-1 \\ \sum_{i=1}^n {f(2*i)} &= f(2)+f(4)+f(5)+\dots+f(2*n) \\ &= f(2*n+1) - 1 \end{aligned}\]

此外，Fibonacci数列还有以下这些有用的性质：

\[\sum_{i=1}^n {f(i)^2} = f(n)*f(n+1)\] \[\sum_{i=1}^n {f(i)*(-1)^i} = (-1)^n * (f(n+1)-f(n))+1\]

常用的还有下列结论：

\[\begin{aligned} f(n+m) &= f(n+1)*f(m) + f(n)*f(m-1) \\ f(2*n+1) &= f(n+1)^2 + f(n)^2 \\ f(2*n) &= 2f(n)f(n+1) - f(n)^2 \\ f(n)^2 &= (-1)^{n+1} + f(n-1)*f(n+1) \end{aligned}\]

由上式稍作变换，便有 $f(m-1)^2 \textit{ mod } f(m) = (-1)^m$

这两个公式都可以通过数学归纳法证明。

题目分析

通过上面的Fibonacci数列前N项求和公式，可以将原来的问题简化成 $f(n)\%f(m)\%p$ 的情形。

\[\begin{aligned} f(n) \textit{ mod } f(m) &= f(n-m+m) \textit{ mod } f(m) \\ &= (f(n-m+1)*f(m)+f(n-m)*f(m-1)) \textit{ mod } f(m) \\ &= f(n-)f(m-1) \textit{ mod } f(m) \\ &= \dots \\ &= f(m-1)^{\frac{n}{m}} f(n \textit{ mod } m) \textit{ mod } f(m) \end{aligned}\]

因此，当 $m$ 的值比较小时，完全可以通过预处理一定范围内的Fibonacci数列，便可以求解出问题的答案。

那么对于本题呢？题目中 $n,m$ 的值都达到了 $10^{18}$，可见，无法通过上面的方面求解。

上文中，我们已经将问题规约为求解 $(f(n+2)-1) \textit{ mod } f(m) \textit{ mod } p$ ，因此，下面将针对这一简化后的问题讨论其解法。因为这一问题与 $f(n+2) \textit{ mod } f(m) \textit{ mod } p$ 等价(仅仅需要将结果减 $1$ 加上 $p$ 然后对 $p$ 取模)，为方便起见，后文主要讨论 $f(n+2) \textit{ mod } f(m) \textit{ mod } p$。

如果 $n+2==m$，那么显然只需要求解出第 $m$ 项的结果即可(因为涉及到 $-1+p$ 对 $f(m)$ 取模)。最终答案应该为

\[f(m) \textit{ mod } p - 1 + p) \textit{ mod } p\]

结合前面提到了快速幂模的方法，这个问题是容易的。我们还有以下结论（推导过程参见文末参考 2）：

当 $k$ 为奇数时，$f(m-1) \times f(k) \textit{ mod } f(m) = f(m-k)$
当 $k$ 为偶数时，$f(m-1) \times f(k) \textit{ mod } f(m) = f(m) - f(m-k)$

如果 $m$ 为偶数，那么如果 $\frac{n}{m}$ 和 $\frac{n}{2m}$ 都是偶数，那么结果应该是： $f(n) \textit{ mod } f(m) = f(n \textit{ mod } m)$
如果 $m$ 为奇数，那么:
- 如果 $\frac{n}{m}$ 和 $\frac{n}{2m}$ 都是偶数，那么结果应该是： $f(n) \textit{ mod } f(m) = f(n \textit{ mod } m)$
- 如果 $\frac{n}{m}$ 是偶数，$\frac{n}{2m}$ 是奇数，那么结果应该是： $f(n) \textit{ mod } f(m) = f(m)-f(n \textit{ mod } m)$
- 如果 $\frac{n}{m}$ 是奇数，$\frac{n}{2m}$ 是偶数，那么结果应该是：
  - 如果 $n \textit{ mod } m$ 是奇数，结果为 $f(n) \textit{ mod } f(m) = f(m-n \textit{ mod } m)$
  - 如果 $n \textit{ mod } m$ 是偶数，结果为 $f(n) \textit{ mod } f(m) = f(m)-f(m-f(n \textit{ mod } m))$
- 如果 $\frac{n}{m}$ 和 $\frac{n}{2m}$ 都是奇数，那么结果应该是：
  - 如果 $n \textit{ mod } m$ 是奇数，结果为 $f(n) \textit{ mod } f(m) = f(m)-f(m-f(n \textit{ mod } m))$
  - 如果 $n \textit{ mod } m$ 是偶数，结果为 $f(n) \textit{ mod } f(m) = f(m-n \textit{ mod } m)$
如果 m 是偶数，那么：
- 如果 $\frac{n}{m}$ 是奇数，那么结果应该是：
  - 如果 $n \textit{ mod } m$ 是奇数，结果为 $f(n) \textit{ mod } f(m) = f(m-n \textit{ mod } m)$
  - 如果 $n \textit{ mod } m$ 是偶数，结果为 $f(n) \textit{ mod } f(m) = f(m)-f(m-f(n \textit{ mod } m))$
- 如果 $\frac{n}{m}$ 是偶数，那么结果应该是： $f(n) \textit{ mod } f(m) = f(n \textit{ mod } m)$

至此，本题基本解决完毕。

其他的细节

这道题的数据量非常大，因此在其他的一些地方也应该充分注意，才有可能通过全部测试点。

使用矩阵快速幂模来求解某一项的值。
64位整数的二进制分解乘法（long long乘以long long会导致溢出）。

long long multiply(long long a, long long b) {
    long long ans = 0;
    a %= MOD;
    while(b) {
        if(b & 1) {
            ans = (ans + a) % MOD;
            b--;
        }
        b >>= 1;
        a = (a + a) % MOD; // a *= 2
    }
    return ans;
}

题目Accept代码：PREV_29.cpp

Fibonacci另一种快速算法

在http://www.zhihu.com/question/29215494看到了另一种基于分治的Fibonacci数列第n项的方法：

double Fibonacci(int n){
    double x = 1.0, y = 1.0, a = 0, b = 1.0,t;
    while (n>0)
    {
        if (n & 1){
            t = a*x + b*y;
            a = x*(b - a) + a*y;
            b = t;
        }
        t = 2 * x*y - x*x;
        y = x*x + y*y;
        x = t;
        n >>= 1;
    }
    return a;
}

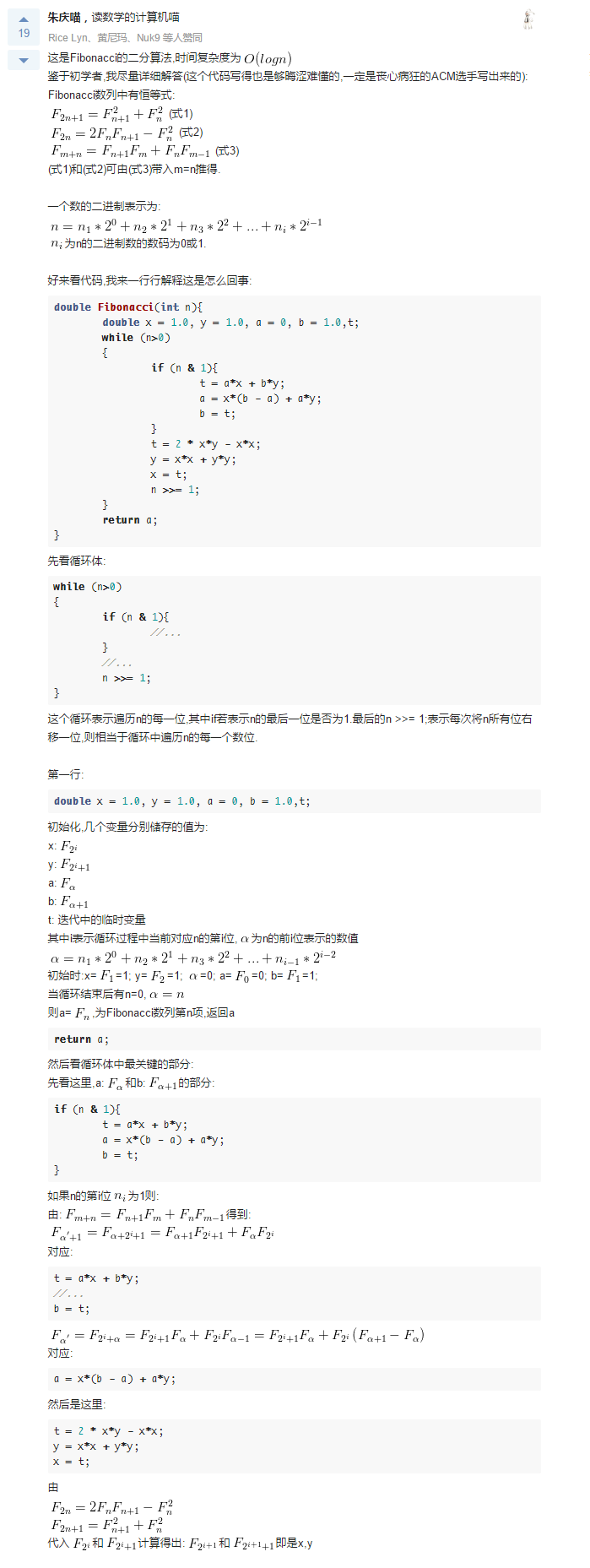
关于该算法的解释如下图所示：

题目

Fibonacci数列

题目分析

其他的细节

Fibonacci另一种快速算法

参考

Comments: